极坐标系

XantC

微分

\[ \begin{align*} &x=r\cos \theta \\ &y=r\sin \theta \\ &\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\frac{\mathrm{d}y}{\mathrm{d}\theta}}{\frac{\mathrm{d}x}{\mathrm{d}\theta}} \\ \end{align*}\]

\[ 平行于极轴\colon{\frac{\mathrm{d}y}{\mathrm{d}\theta}}=0 \]

\[ 垂直于极轴\colon{\frac{\mathrm{d}x}{\mathrm{d}\theta}}=0 \]

积分

\[ \mathrm{S}=\frac{1}{2}\int_{\alpha}^{\beta}r^2\mathrm{d}\theta \]

证明

\[ \begin{align*} \mathrm{S}&=\sum_{i=0}^{+\infty}\frac{1}{2}r^2\mathrm{d}\theta_{i} \\ &=\frac{1}{2}\int_{\alpha}^{\beta}r^2\mathrm{d}\theta \end{align*} \]

作图

\[ 对于r=a(p+q\cos\theta)\enspace(p\geq q) \colon \]

当\(p=q \colon\)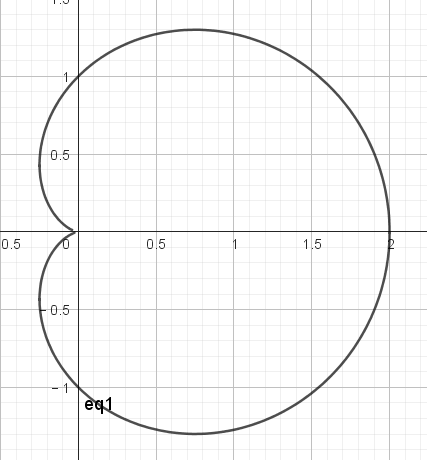

当\(q<p<2q \colon\)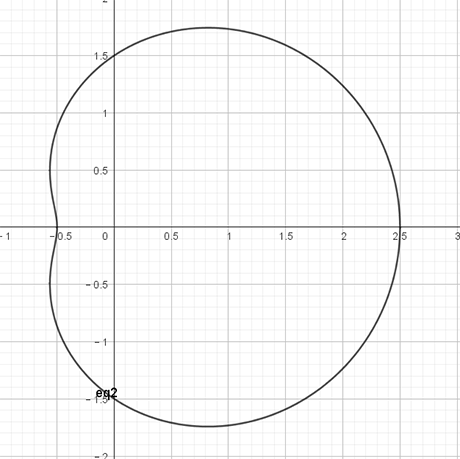

当\(p\geq 2q \colon\)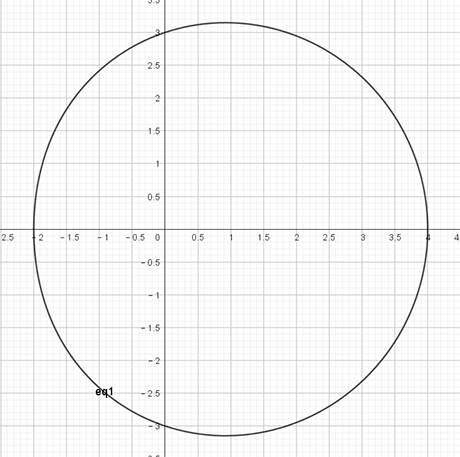

证明

证明图像有没有凹口，相当于证它切线垂直于极轴的点的个数大于2

证明：

\[ x=r\cos\theta=a\cos\theta(p+q\cos\theta) \]

\[ x=ap\cos\theta+aq\cos^2\theta \]

\[\frac{\mathrm{d}x}{\mathrm{d}\theta}=-ap\sin\theta-2aq\sin\theta\cos\theta=0\]

\[ \sin\theta=0\enspace\mathrm{or}\;\cos\theta=-\frac{p}{2q} \]

Case 1 有凹口

\[ \mathrm{Case}\ 1.1\colon\enspace p=q \]

\[ \therefore -\frac{p}{2q}=-\frac{1}{2} \]

\[ \therefore \theta=0,\pi,\pm\frac{2}{3}\pi \]

其中\(\theta=\pi\)时，\(\frac{\mathrm{d}y}{\mathrm{d}\theta}\)和\(\frac{\mathrm{d}x}{\mathrm{d}\theta}\)都为零，再观察图像，发现切线其实是平行于极轴的，所以\(\theta=0,\pm\frac{2}{3}\pi\),有凹口

\[ ~ \]

\[ \mathrm{Case}\ 1.2\colon\enspace q<p<2q \]

\[ \therefore -1<-\frac{p}{2q}<1 \]

\[ \therefore \theta=0,\pi,\arccos(-\frac{p}{2q}),(2\pi-\arccos(-\frac{p}{2q})) \]

\(\theta\)有四个解，所以图像有凹口

Case 2 无凹口

\[ \mathrm{Case}\ 2\colon\enspace p\geq2q \]

\[ \therefore -\frac{p}{2q}\leq-1 \]

\[ \because\sin\theta=0\enspace\mathrm{or}\;\cos\theta=-\frac{p}{2q}\]

\[ \therefore \theta=0,\pi \]

\(\theta\)有两个解，所以图像无凹口