spiral motion in magnetic field
This article is here to clear up a misunderstanding: physics problems can be solved with mathematical tools alone. Recently I've struggled to explain spiral motion in magnetic field using only the cross product, and eventually discovered a clearer way to express what it actually is.
First consider the Lorentz force:
\[ \boldsymbol{F}=q\boldsymbol{v}\times\boldsymbol{B} \]
In vector algebra, this can be interpreted as either below:
\[ \boldsymbol{F}=q\boldsymbol{v_{\perp}}\times\boldsymbol{B} \quad \text{or} \quad \boldsymbol{F}=q\boldsymbol{v}\times\boldsymbol{B_\perp} \]
Since each interpretation (or decomposition of vector) is true in math, one might easily jump into the idea that when dealing with non-vertical \(\boldsymbol{v}\) and \(\boldsymbol{B}\), he can decompose either of them and consider only the perpendicular component. But this isn't the right way. In terms of magnetic force, it is clearly stated that the field only acts on the the perpendicular component of velocity, rather than the other way around. This can be shown by the examination on spiral motion (which I guess is the key to disclose the 'which one to decompose' mystery).
All positive charge here.
Approach 1: do the \(\boldsymbol{B}\)
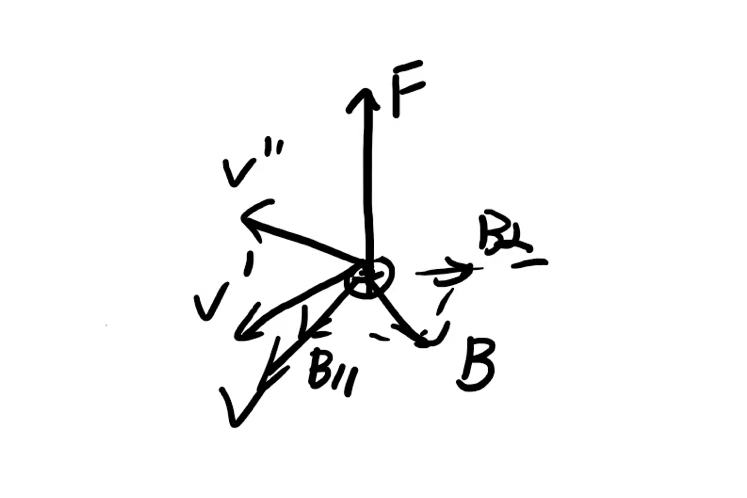
The graph looks extremely weird. We can draw out the \(\boldsymbol{F}\) at the very moment our charge is placed in the field. Since it acts on \(\boldsymbol{v}\), we can find that it will rotate upwards (we keep the position of the charge fixed which counts for nothing but the change of the direction of velocity), until the moment when it points the same way as the original force, becomes vertical to \(\boldsymbol{B}\), hence starting rotating in a circular path. Through this analysis, it appears that the charge will eventually do circular motion, and "spiral", which is found in experiments, is completely invisible in our deduction.
Approach 2: do the \(\boldsymbol{v}\)
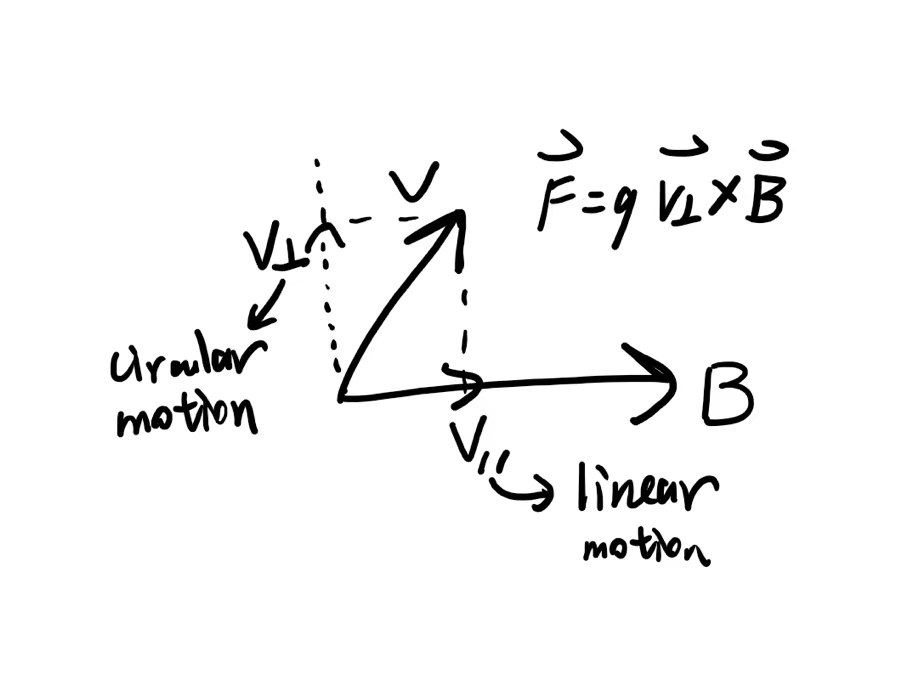
From the graph we can find two separate motions: circular motion on a plane (whose normal vector is \(\boldsymbol{B}\)), and linear motion along the parallel component of \(\boldsymbol{v}\). Spiral motion is the combination of both: circular on a plane, linear along its normal.
And if we dig a little deeper, this actually unveils how magnetic field produces force on charges with velocity: it grasps its component vertical to it, creates a force with vector product, which only acts on the velocity from which it results. That is, though Lorentz force is not only vertical to the vertical velocity but surprisingly to the entire one, it does not make the whole rotate, but only the part of it. This is how magnetic works. It cares naught for what the parallel part of velocity is going on, but only the vertical. And the force acts so as well.
Therefore, I prefer writing Lorentz force in this way after making this mess clear:
\[ \boldsymbol{F} = q\boldsymbol{v_{\perp}}\times\boldsymbol{B} \]
Though it seems that I saved some work of the cross product by writing the prep explicitly, what I actually mean is it's not up to us to choose which vector to break down (This on Monday and that on Tuesday). It can only be \(\boldsymbol{v}\), and I need it directly stated in the formula, with no misconceptions.